Wie groß ist die mittlere Geschwindigkeit des Fahrzeugs zwischen zwei Zeitpunkten
Wie groß ist die mittlere Geschwindigkeit des Fahrzeugs
zwischen zwei Zeitpunkten ![]() und
und ![]() ?
?
LöSUNG:
![]()
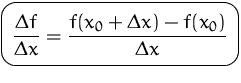
Dieser Ausdruck heißt Differenzenquotient.
Graphische Bedeutung des Differenzenquotienten:
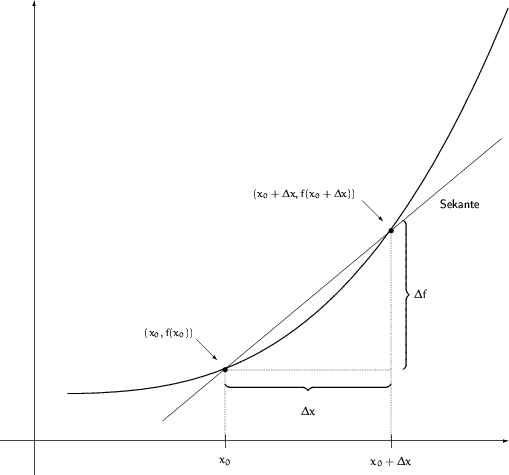
Wie groß ist die momentane Geschwindigkeit des Autos zum
Zeitpunkt ![]() ?
?
LöSUNG:
Wir können die mittlere Geschwindigkeit des Autos zwischen den
Zeitpunkten ![]() und
und ![]() für ein möglichst kleines
für ein möglichst kleines ![]() berechnen.
Je kleiner dieses
berechnen.
Je kleiner dieses ![]() ist desto eher wird der Differenzenquotient mit
der Momentangeschwindigkeit übereinstimmen.
ist desto eher wird der Differenzenquotient mit
der Momentangeschwindigkeit übereinstimmen.
DEFINITION (DIFFERENTIALQUOTIENT)
Falls der Limes
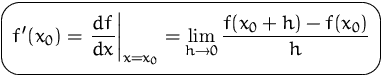
existiert, so heißt die Funktion ![]() differenzierbar
an der Stelle
differenzierbar
an der Stelle ![]() und dieser Grenzwert
Differentialquotient oder (erste) Ableitung der
Funktion an der Stelle
und dieser Grenzwert
Differentialquotient oder (erste) Ableitung der
Funktion an der Stelle ![]() .
.
Eine Funktion ![]() heißt differenzierbar, wenn
sie in jedem Punkt des Definitionsbereichs differenzierbar ist.
heißt differenzierbar, wenn
sie in jedem Punkt des Definitionsbereichs differenzierbar ist.