In vielen Fällen ist eine Kenngröße nur zu bestimmten
diskreten Zeitenpunkten ![]() bekannt.
bekannt.
Wir beschreiben die Kenngröße durch eine Abbildung
![]() , i.e. eine Folge
Schreiben
, i.e. eine Folge
Schreiben ![]() anstatt
anstatt ![]() .
.
Wir müssen Differentialquotienten ![]() durch den
Differenzenquotienten
durch den
Differenzenquotienten
![]() ersetzen.
ersetzen.
Unter der Annahme, daß ![]() nur ganzzahlige Werte annimmt
(d.h.
nur ganzzahlige Werte annimmt
(d.h. ![]() ),
dann wird aus diesem Differenzenquotient die
ersten Differenz
),
dann wird aus diesem Differenzenquotient die
ersten Differenz ![]() .
.
Diese Differenz hängt davon ab, zwischen welchen Zeitpunkten diese Differenz gebildet wird. Schreiben daher:
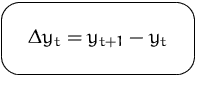
Die ![]() -ten Ableitung
-ten Ableitung ![]() ersetzen wir durch die
Differenz der Ordnung
ersetzen wir durch die
Differenz der Ordnung ![]() :
:
![]()
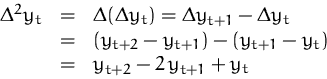
DEFINITION (DIFFERENZENGLEICHUNG)
Eine Differenzengleichung ist eine Gleichung, die
eine Differenz enthält. Sie heißt von
![]() -ter Ordnung, wenn die höchste Ordnung der vorkommenden Differenzen
gleich
-ter Ordnung, wenn die höchste Ordnung der vorkommenden Differenzen
gleich ![]() ist.
ist.
BEISPIEL
![]()
Differenzengleichung erster Ordnung
![]()
Differenzengleichung erster Ordnung
![]()
Differenzengleichung zweiter Ordnung
Für Differenzen gelten ähnliche Rechenregeln wie für Differentialquotienten:
| Summenregel | |
| Produktregel | |
| Quotientenregel | |
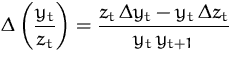 |
Äquvalente Darstellung für Differenzengleichungen enthält
keinen ![]() -Ausdruck
(wird im folgenden verwendet).
-Ausdruck
(wird im folgenden verwendet).
BEISPIEL
Die Differenzengleichungen aus obigen
Beispiel lassen sich darstellen als
![]()
![]()
![]()
![]()
![]()
Aufgabe:
Finde eine Folge ![]() , die die angegebene Rekursionsformel
für alle
, die die angegebene Rekursionsformel
für alle ![]() erfüllt.
erfüllt.