| (3') | Optimalitätstest:
Alle Koeffizienten in der ZFZ sind
|
|---|---|
| (4') | Pivotspalte: größter Eintrag in ZFZ. |
Das Standard-Minimierungsproblem ist vollkommen analog zum Maximierungsproblem. Wir müssen nun aber entgegen der Richtung des Gradienten wandern. Daraus ergibt sich folgende Änderung der Vorgangsweise in den Punkten (3) und (4).
(Alle anderen Punkte sind identisch!)
| (3') | Optimalitätstest:
Alle Koeffizienten in der ZFZ sind
|
|---|---|
| (4') | Pivotspalte: größter Eintrag in ZFZ. |
BEISPIEL
![\begin{displaymath}
\begin{array}
{rcl}
z(x_1,x_2,x_3) = 3\,x_1 + 2\,x_2 +4\,x_...
...1 + 2\,x_3 &\geq& -1 \\ [1ex]
x_1,\,x_3 &\geq& 0
\end{array} \end{displaymath}](img1493.gif)
Anfangs-Simplex-Tableau aufstellen:
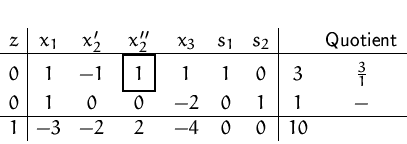
Die Basislösung dieses Tableaus ist zulässig:
![]() .
.
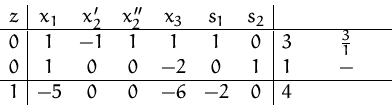
Alle Einträge in der Zielfunktionszeile sind ![]() . Wir haben daher das Minimum erreicht.
. Wir haben daher das Minimum erreicht.
Die minimale zulässige Basislösung lautet
![]()
Das Minimum liegt somit im Punkt
![]() .
.